CAPITALIZACIÓN SIMPLE
OPERACIÓN FINANCIERA:
Una operación financiera es toda acción encaminada a la sustitución, en un momento determinado del tiempo, de uno o varios capitales por otro u otros equivalentes en diferentes momentos del tiempo, aplicando una determinada ley financiera.
SUJETOS:
- Acreedor o prestamista: parte que entrega el primer capital. El conjunto de entregas realizadas por el prestamista se denomina prestación.
- Deudor o prestatario: parte que recibe el primer capital. El conjunto de pagos a realizar por el prestatario se denomina contraprestación.
Las leyes financieras son expresiones o modelos matemáticos que nos permiten cuantificar los intereses por el aplazamiento y/o anticipación de un capital futuro.
Respecto a las leyes financieras distinguimos:
- Leyes financieras en régimen de simple: en las que los intereses no son productivos, es decir, los intereses producidos no se acumulan al capital de partida para producir a su vez nuevos intereses.
- Leyes financieras en régimen de compuesta: en la que los interese se van acumulando de un periodo a otro, es decir, se calculan sobre el capital inmediatamente anterior. Se trata de intereses productivos.
CLASIFICACIÓN DE LAS OPERACIONES FINANCIERAS.
Las operaciones financieras pueden clasificarse según diferentes criterios. Los más interesantes para nuestro estudio son:
- Según la certeza de la cuantía y el vencimiento:
- Ciertas. Cuando cuantía y vencimiento están determinadas. Sólo veremos estas.
- Aleatorias. Cuando se desconoce cuantía, o vencimiento o ambas.
- Según la duración de la operación:
- A corto plazo, operaciones que duran un año o menos.
- A largo plazo, operaciones que duran más de un año.
- Según el número de capitales que intervienen en la operación:
- Simples, cuando hay un sólo capital en prestación y contraprestación.
- Compuestas, en caso contrario al anterior. Pueden ser:
- de constitución, cuando hay varios capitales en la prestación y uno sólo en la contraprestación al final de la duración.
- de amortización, cuando hay un sólo capital en la prestación al inicio de la operación y varios en la contraprestación.
- Según la ley financiera:
- Capitalización, cuando los vencimientos de todos los capitales son anteriores o iguales al momento de tiempo que se sustituyen o se comparan los capitales.
- Descuento o actualización, cuando los vencimientos de todos los capitales son posteriores al momento del tiempo en el que se realiza la comparación o sustitución
1. CAPITALIZACIÓN SIMPLE:
1.1.1. Concepto
Operación financiera cuyo objeto es la sustitución de un capital presente por otro equivalente con vencimiento posterior, mediante la aplicación de la ley financiera en régimen de simple.
1.1.2. Descripción de la operación
Partiendo de un capital (C0) del que se dispone inicialmente -capital inicial-, se trata de determinar la cuantía final (Cn) que se recuperará en el futuro sabiendo las condiciones en las que la operación se contrata (tiempo -n- y tipo de interés -i-).
Este capital final o montante se irá formando por la acumulación al capital inicial de los intereses que genera la operación periódicamente y que, al no disponerse de ellos hasta el final de la operación, se añaden finalmente al capital inicial.
1.1.3. Características de la operación
Los intereses no son productivos, lo que significa que:
- A medida que se generan no se acumulan al capital inicial para producir nuevos intereses en el futuro y, por tanto
- Los intereses de cualquier período siempre los genera el capital inicial, al tanto de interés vigente en dicho período.
Gráficamente para una operación de tres períodos:
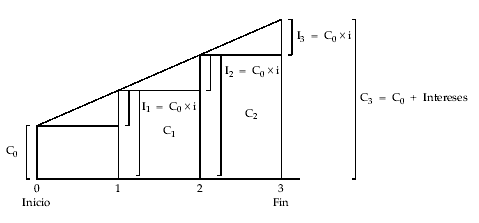
1.1.4. Desarrollo de la operación
El capital al final de cada período es el resultado de añadir al capital existente al inicio del mismo los intereses generados durante dicho período. De esta forma, la evolución del montante conseguido en cada momento es el siguiente:
| Momento 0: C0 Momento 1: C1 = C0+ I1 = C0 + C0x i = C0x (1 + i) Momento 2: C2 = C0+ I1 + I2 = C0 + C0x i + C0x i = C0x (1 + 2 i) Momento 3: C3 = C0 + I1 + I2 + I3 = C0 + C0x i + C0x i + C0 i = C0x (1 + 3 i) ... Momento n: Cn = C0 + I1 + I2 + ... + In = C0 + C0x i + ... + C0x i = C0 + C0x nxi |
| Cn = C0 x (1 + n x i) |
Expresión aplicable cuando el tipo de interés de la operación se mantiene constante todos los períodos.
A partir de la expresión anterior (denominada fórmula fundamental de la capitalización simple) no solamente se pueden calcular montantes sino que, conocidos tres datos cualesquiera, se podría despejar el cuarto restante.
Finalmente, hay que tener en cuenta que «n» lo que indica es el número de veces que se han generado (y acumulado) intereses al capital inicial, por tanto, esa variable siempre ha de estar en la misma unidad de tiempo que el tipo de interés (no importando cuál sea).
EJEMPLO 1
Calcular el montante obtenido al invertir 2.000 euros al 8% anual durante 4 años en régimen de capitalización simple.
C4 = 2.000 x (1 + 4 x 0,08 ) = 2.640 €
EJEMPLO 2
Se quiere conocer qué capital podremos retirar dentro de 3 años si hoy colocamos 1.000 euros al 5% de interés anual para el primer año y cada año nos suben el tipo de interés un punto porcentual.
En este caso la fórmula general de la capitalización simple no es aplicable al ser diferente el tipo de interés en cada período. El montante será, igualmente, el resultado de añadir al capital inicial los intereses de cada período, calculados siempre sobre el capital inicial pero al tipo vigente en el período de que se trate.
C3 = C0 + I1 + I2 + I3 = 1.000 + 1.000 x 0,05 + 1.000 x 0,06 + 1.000 x 0,07 = 1.180 €
1.1.5. Cálculo del capital inicial
Partiendo de la fórmula de cálculo del capital final o montante y conocidos éste, la duración de la operación y el tanto de interés, bastará con despejar de la misma:
Cn = C0 x (1 + n x i)
despejando C0 resulta:

EJEMPLO 3
¿Cuánto deberé invertir hoy si quiero disponer dentro de 2 años de 1.500 euros para comprarme un coche, si me aseguran un 6% de interés anual para ese plazo?

1.1.6. Cálculo de los intereses totales
Bastará con calcular los intereses de cada período, que siempre los genera el capital inicial y sumarlos.
Intereses totales = I1 + I2 + ... + In = C0x i1 + C0x i2 + ... + C0x in
| C0 x (i1 + i2 + ... + in) |
Si i1 = i2 = ... = in = i se cumple:
Intereses totales = I1 + I2 + ... + In = C0x i + C0x i + ... + C0x i
| IT = C0 x i x n |
Conocidos los capitales inicial y final, se obtendrá por diferencias entre ambos:
| In = Cn - C0 |
EJEMPLO 4
¿Qué intereses producirán 300 euros invertidos 4 años al 7% simple anual?
Por suma de los intereses de cada período:
Intereses totales = I1 + I2 + I3 + I4 = C0x i + C0x i + C0x i + C0x i = C0 x i x 4 = 300 x 0,07 x 4 = 84 €
También se puede obtener por diferencias entre el capital final y el inicial:
C4 = 300 x (1 + 0,07 x 4) = 384
In = 384 - 300 = 84 €
EJEMPLO 5
¿Qué interés producirán 6.000 euros invertidos 8 meses al 1% simple mensual?
In = C0 x i x n = 6.000 x 0,01 x 8 = 480 €
1.1.7. Cálculo del tipo de interés
Si se conocen el resto de elementos de la operación: capital inicial, capital final y duración, basta con tener en cuenta la fórmula general de la capitalización simple y despejar la variable desconocida.
Cn = C0 x (1 + n x i)
Los pasos a seguir son los siguientes:
Pasar el C0 al primer miembro:

Pasar el 1 al primer miembro (restar 1 en los dos miembros):

Despejar el tipo de interés, dividiendo por n la expresión anterior:

EJEMPLO 6
Determinar el tanto de interés anual a que deben invertirse 1.000 euros para que en 5 años se obtenga un montante de 1.500 euros.

1.1.8. Cálculo de la duración
Conocidos los demás componentes de la operación: capital inicial, capital final y tipo de interés, partiendo de la fórmula general de la capitalización simple y despejando la variable desconocida.
Punto de partida:
Cn = C0 x (1 + n x i)
Pasar el C0 al primer miembro:
Cn/Co = (1 + n x i)
Pasar el 1 al primer miembro (restar 1 en los dos miembros):
Cn/Co -1 = n x i
Despejar la duración n, dividiendo por i:

EJEMPLO 7
Un capital de 2.000 euros colocado a interés simple al 4% anual asciende a 2.640 euros. Determinar el tiempo que estuvo impuesto.
TANTOS EQUIVALENTES:
Normalmente los tipos de interés suelen venir expresados en términos anuales, pero no siempre se devengan con esa periodicidad, sino que, en la mayoría de las ocasiones, la acumulación de los intereses al capital inicial se hace en períodos más pequeños (meses, trimestres, semestres, ...).
La cuestión es ¿por el hecho de modificar la frecuencia de cálculo de intereses me beneficiaré o, por el contrario, me veré perjudicado? En este sentido, lo lógico es pensar que cualquiera que sea el número de veces que se calculen los intereses, al final el importe total de los mismos no haya variado, esto es, el resultado final de la operación no se vea afectado.
En consecuencia, si se cambia la frecuencia de cálculo de los intereses habrá que cambiar el importe del tanto de interés aplicado en cada caso. Surge el concepto de tantos equivalentes.
1.2.1. Concepto
Dos tantos cualesquiera, expresados en distintas unidades de tiempo, se dice que son tantos equivalentes cuando aplicados a un mismo capital inicial durante un mismo período de tiempo producen el mismo interés o generan el mismo capital final o montante.
1.2.2. Relación de tantos equivalentes
Los tantos de interés equivalentes en simple son proporcionales, es decir, cumplen la siguiente expresión:
| i = ik x k |
donde k se denomina frecuencia de capitalización y se define como el número de partes iguales en las que se divide el período de referencia (considerando como tal el año), pudiendo tomar los siguientes valores:
k = 2 -> semestre i2 = tanto de interés semestral
k = 3 -> cuatrimestre i3 = tanto de interés cuatrimestral
k = 4 -> trimestre i4 = tanto de interés trimestral
k = 12 -> mes i12 = tanto de interés mensual
EJEMPLO 8
Determinar el montante resultante de invertir 700 euros durante 3 años en las siguientes condiciones:
a) Interés anual del 12%
Cn = 700 x (1 + 3 x 0,12) = 952 €
b) Interés semestral del 6%
Cn = 700 x (1 + 3 x 0,06 x 2) = 952 €
c) Interés mensual del 1%
Cn = 700 x (1 + 3 x 0,01 x 12) = 952 €