Esta historia empieza como muchas otras de matemáticas: con Pitágoras. Pero el final de la historia se encuentra en un lugar muy, muy lejano: el teorema de los tres pasos. Quieres saber qué es el teorema de los tres pasos y qué tiene que ver todo esto con las escalas musicales? ¡sigue leyendo!

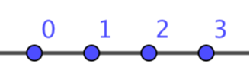
Supongamos que hacemos sonar una cuerda tensa de longitud L. Los pitagóricos descubrieron que el sonido más consonante que se puede construir con la anterior cuerda se produce dividiéndola en dos partes iguales. En términos modernos, si una vibra con una frecuencia f, la otra lo hará con una frecuencia 2f. A este intervalo se le llama OCTAVA. Si repetimos este proceso de dividir a la mitad la longitud de nuestra cuerda una y otra vez, habremos  obtenido una sucesión geométrica de razón 2 y primer término f:

Podemos dar por hecho que el origen de nuestra secuencia es f, y dividir cada frecuencia por f. Nos estamos quedando con los intervalos de octava:

Pero claro, quedaría todo mucho más mono si tomamos logaritmo en base 2, de esa forma las longitudes entre octavas serían las mismas y la sucesión de logaritmos de intervalos pasa a ser la de los números naturales:

En realidad hay un motivo importante para trabajar con logaritmos de frecuencias al estudiar los sonidos: la relación entre percepción y estímulo en el oído es logarítmica. Es la conocida como ley de Weber-Fechner. Pero bueno, no nos vamos a meter en los mundos de la psico-acústica en esta entrada. ¡Sólo faltaría!

Ahora viene el paso clave, ¡¡¡atención!!! Cómo los pitagóricos decían, el intervalo de octava es el más consonante, tanto es así que podemos identificar todos los sonidos cuya distancia es una serie de octavas, esto es, podemos aplicar sobre las frecuencias de sonidos la siguiente relación de equivalencia:

$f ~ f\text{'} \iff f= 2^{k}f\text{'} con k\in \mathrm{\mathbb{Z}}$

Y después, claro tomamos logaritmo en base 2. Identificar en $\mathrm{ℝ}$ el conjunto de números enteros $\mathrm{\mathbb{Z}}$ supone, aritméticamente, trabajar con partes decimales: {x}=x-[x].

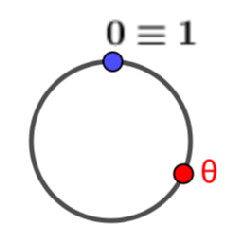Geométricamente todo es mucha más chulo: el conjunto cociente $\mathrm{ℝ}/\mathrm{\mathbb{Z}}$ se puede pensar como el círculo de longitud unidad.

Si te has perdido un poco, no te preocupes, todo el proceso se resume de una forma muy sencilla: al 0 en el círculo le asignamos una nota de partida (por ejemplo el La) que representa en realidad un conjunto infinito de notas (todos los La, esto es todas las notas de frecuencias 440Hz·2^k). Cualquier otra nota $\theta$ se representa por un punto del círculo unidad. Esa nota, aritméticamente es un número decimal entre 0 y 1. 

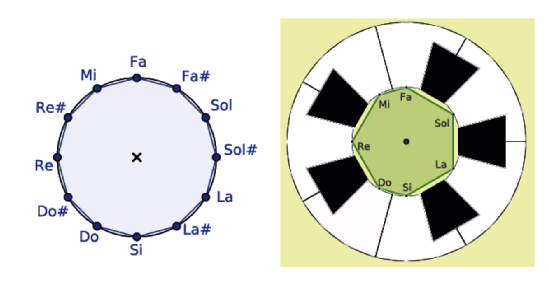
Y a partir de aquí viene lo chulo, chulo de verdad. Podemos pensar las escalas musicales como polígonos inscritos en la circunferencia. Por ejemplo, la escala de las teclas del piano (la escala cromática) sería el polígono regular de 12 vértices, mientras que si nos quedamos con las teclas blancas nada más (escala diatónica), tendríamos un subconjunto de vértices de este polígono regular:

Volvamos un segundo a los pitagóricos para dar una última vuelta de tuerca a la construcción geométrica de las escalas. ¿Cuál es el segundo intervalo más consonante? La quinta. La obtenemos haciendo sonar 2 tercios de la cuerda tensa de longitud L. La frecuencia sería $\frac{3}{2}f$. Dividiendo por f y tomando logaritmos en base dos, nuestro punto en el círculo será ${\log }_2\left(\frac{3}{2}\right)\simeq 0.58496...$ 

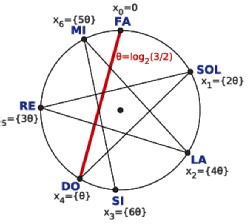
Este es el intervalo de quinta pura. Si generamos escalas con la quinta pura como nota de partida, geométricamente estaremos construyendo polígonos estrellados (líneas poligonales, en realidad).

En la figura se muestra la escala de 7 notas generada por la quinta pura. Aritméticamente estamos calculando la parte decimal {x} de la sucesión  k$\theta$, con k=0,1,2.... Observa que si calculásemos la octava nota {7$\theta$} NO volveríamos al punto de partida x₀=0. Eso es debido a que $3^s =2^r$ no tiene soluciones enteras. Y este hecho tiene implicaciones musicales tremendas: la escala generada por quintas no termina de encajar en las octavas. Este es el origen matemático de los temperamentos musicales. De nuevo, no es este post lugar para hablar de un asunto tan complicado.

¿Qué pasará sin en lugar de coger el generador de la escala ${\log }_2\left(\frac{3}{2}\right)\simeq 0.58496...$ cogemos un número cualquiera $\theta \in (0,1)$ y si en lugar de generar 7 notas generamos N? Pues gracias al Geogebra puedes comprobarlo tú mismo:

A partir de aquí: ESPOILER FINAL. Si te fijas en el número de intervalos distintos que tiene la escala al ir cambiando $\theta y N$, verás que los puede haber azules, rojos o negros. Pero nunca va a haber más de tres intervalos distintos. A esto se le llama teorema de los tres pasos (three-gap theorem) y es un resultado especialmente hermoso: con una descripción geométrica super sencilla, tiene múltiples aplicaciones y conexiones con nociones matemáticas más complejas. 

Nos podemos hacer muchas preguntas en este punto, ¿cuándo aparecen exactamente 2 intervalos distintos y no tres? ¿cómo es la secuencia de intervalos largo y cortos en ese caso? ¿qué tiene que ver eso con el valor decimal del generador elegido de la escala?

En fin, sólo diré que para dar respuesta a todas esas preguntas se necesitan los desarrollos en fracciones continuas del generador, así como  nociones de secuencias de Sturm y palabras de Christoffel. Pero este post va siendo demasiado largo ya...tendremos que esperar para adentrarnos en el mundo de la combinatoria algebraica de palabras.

Y una NOTA FINAL: el próximo año se celebra la séptima edición del congreso internacional Mathematics and Computation in Music. Esta vez toca en Madrid, aquí cerquita. Es una ocasión única para poder ponerse al día en los últimos avances científicos de este campo.

Este post forma parte del Carnaval de Matemáticas, que en esta edición 79, denominada 9.3 está organizado por @juanfisicahr a través de su blog Esto no entra en el examen.