CAPITALIZACIÓN COMPUESTA
1. CAPITALIZACIÓN COMPUESTA
1.1. CONCEPTO
Operación financiera cuyo objeto es la sustitución de un capital por otro equivalente con vencimiento posterior mediante la aplicación de la ley financiera de capitalización compuesta.
1.2. DESCRIPCIÓN DE LA OPERACIÓN
El capital final (montante) (Cn) se va formando por la acumulación al capital inicial (C0) de los intereses que periódicamente se van generando y que, en este caso, se van acumulando al mismo durante el tiempo que dure la operación (n), pudiéndose disponer de ellos al final junto con el capital inicialmente invertido.
1.3. CARACTERÍSTICAS DE LA OPERACIÓN
Los intereses son productivos, lo que significa que:
- A medida que se generan se acumulan al capital inicial para producir nuevos intereses en los períodos siguientes.
- Los intereses de cualquier período siempre los genera el capital existente al inicio de dicho período.
Gráficamente para una operación de tres períodos:
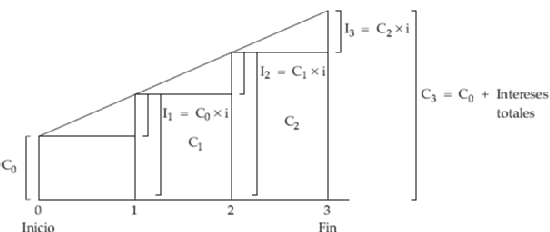
1.4. DESARROLLO DE LA OPERACIÓN
El capital al final de cada período es el resultado de añadir al capital existente al inicio del mismo los intereses generados durante dicho período. De esta forma, la evolución del montante conseguido en cada momento es el siguiente:
| Momento 0: C0
|
Expresión que permite calcular el capital final o montante (Cn) en régimen de compuesta, conocidos el capital inicial (C0), el tipo de interés (i) y la duración (n) de la operación.
Expresión aplicable cuando el tipo de interés de la operación no varía. En caso contrario habrá que trabajar con el tipo vigente en cada período.
A partir de la expresión anterior (denominada fórmula fundamental de la capitalización compuesta) además de calcular montantes, podremos, conocidos tres datos cualesquiera, despejar el cuarto restante.
EJEMPLO 1
Calcular el montante obtenido al invertir 200 euros al 5% anual durante 10 años en régimen de capitalización compuesta.
C10 = 200 x (1 + 0,05)10 = 325,78 €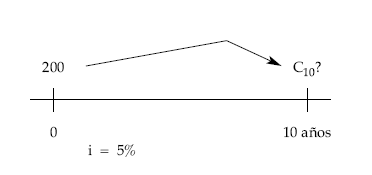
Si se hubiese calculado en simple:
C10 = 200 x (1 + 0,05 x 10) = 300 €
La diferencia entre los dos montantes (25,78 euros) son los intereses producidos por los intereses generados y acumulados hasta el final.
1.5. CÁLCULO DEL CAPITAL INICIAL
Partiendo de la fórmula de cálculo del capital final o montante y conocidos éste, la duración de la operación y el tanto de interés, bastará con despejar de la misma:
Cn = C0 x (1 + i)n
de donde se despeja C0:
Co = Cn / (1+n x i)
EJEMPLO 2
¿Cuánto deberé invertir hoy si quiero disponer dentro de 2 años de 1.500 euros para comprarme un coche, si me aseguran un 6% de interés anual compuesto para ese plazo?
| C0 = | 1.500 | = 1.334,99 € |
1.6. CÁLCULO DE LOS INTERESES TOTALES
Conocidos los capitales inicial y final, se obtendrá por diferencia entre ambos:
| In = Cn – C0 |
EJEMPLO 3
¿Qué intereses producirán 300 euros invertidos 4 años al 7% compuesto anual?
C4 = 300 x (1 + 0,07)4 = 393,24 €
In = 393,24 – 300 = 93,24 €
1.7. CÁLCULO DEL TIPO DE INTERÉS
Si se conoce el resto de elementos de la operación: capital inicial, capital final y duración, basta con tener en cuenta la fórmula general de la capitalización compuesta y despejar la variable desconocida.
Cn = C0 x (1 + i)n
Los pasos a seguir son los siguientes:
- Pasar el C0 al primer miembro:
Cn
---- = (1 + i)n
C0 - Quitar la potencia (extrayendo raíz n a los dos miembros):
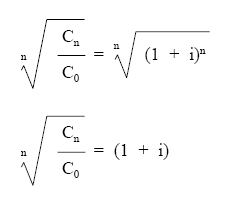
- Despejar el tipo de interés:
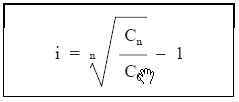
EJEMPLO 4
Determinar el tanto de interés anual a que deben invertirse 1.000 euros para que en 12 años se obtenga un montante de 1.601,03 euros.
1.000 x (1 + i) 12 = 1.601,03
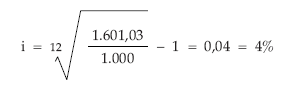
1.8. CÁLCULO DE LA DURACIÓN
Conocidos los demás componentes de la operación: capital inicial, capital final y tipo de interés, basta con tener en cuenta la fórmula general de la capitalización compuesta y despejar la variable desconocida.
- Partiendo de la ecuación inicial y pasando C0 al primer miembro:
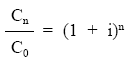
- Tomando logaritmos a ambos lados de la igualdad:
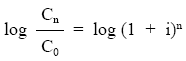
- Aplicando las propiedades de los logaritmos:
![]()
- Despejar la duración:
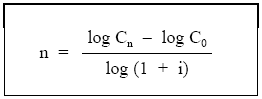
EJEMPLO 5
Un capital de 2.000 euros colocado a interés compuesto al 4% anual asciende a 3.202 euros. Determinar el tiempo que estuvo impuesto.
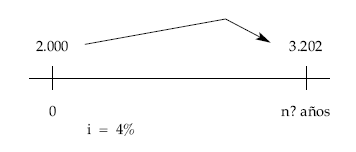
2.000 x (1 + 0,04 )n = 3.202
| n = | log Cn – log C0 | log 3.202 – log 2.000 | = 12 años |
1.9. ESTUDIO COMPARATIVO DE LA CAPITALIZACIÓN SIMPLE Y COMPUESTA
Si el estudio se realiza con un capital de 1.000 euros colocados a un tipo del 10% efectivo anual, durante 6 años, el siguiente cuadro recoge el montante alcanzado al final de cada período en un caso y otro
| Años | 1 | 2 | 3 | 4 | 5 | 6 |
| En simple.......... | 1.100,00 | 1.200,00 | 1.300,00 | 1.400,00 | 1.500,00 | 1.600,00 |
| En compuesta... | 1.100,00 | 1.210,00 | 1.331,00 | 1.464,10 | 1.610,51 | 1.771,56 |
Donde se observa que el montante obtenido en régimen de simple va aumentando linealmente, cada año aumentan 100 euros (los intereses del año, generados siempre por el capital inicial de 1.000 euros). Por su parte, en la operación en compuesta, cada año se van generando más intereses que en el período anterior: la evolución no es lineal sino exponencial, consecuencia de ser el capital productor de los mismos cada año mayor (los intereses generan nuevos intereses en períodos siguientes).
Gráficamente:
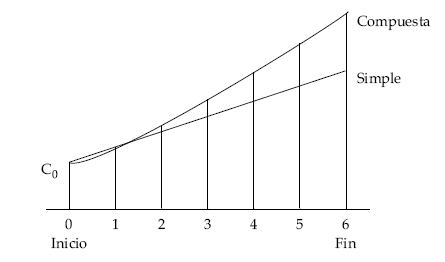
Transcurrido un período (1 año si se considera tipos anuales) el montante coincide en ambos regímenes, para cualquier otro momento ya no existe ninguna coincidencia, siendo las diferencias entre ambos sistemas cada vez mayores.
De la misma forma, se cumple que para períodos inferiores al año el montante es mayor en régimen de simple y, a partir del año, es mayor en compuesta. Éste es el motivo de la preferencia de la capitalización simple en operaciones a corto plazo y la compuesta para el largo plazo.
2. TANTOS EQUIVALENTES
La definición de tantos equivalentes es la misma que la vista en régimen de simple, esto es, dos tantos cualesquiera, expresados en distintas unidades de tiempo, son tantos equivalentes cuando aplicados a un mismo capital inicial y durante un mismo período de tiempo producen el mismo interés o generan el mismo capital final o montante.
Como ya se comentó cuando se hablaba del interés simple, la variación en la frecuencia del cálculo (y abono) de los intereses suponía cambiar el tipo de interés a aplicar para que la operación no se viera afectada finalmente. Entonces se comprobó que los tantos de interés equivalentes en simple son proporcionales, es decir, cumplen la siguiente expresión:
i = ik x k
Sin embargo, esta relación de proporcionalidad no va a ser válida en régimen de compuesta, ya que al irse acumulando los intereses generados al capital de partida, el cálculo de intereses se hace sobre una base cada vez más grande; por tanto, cuanto mayor sea la frecuencia de capitalización antes se acumularán los intereses y antes generarán nuevos intereses, por lo que existirán diferencias en función de la frecuencia de acumulación de los mismos al capital para un tanto de interés dado.
Este carácter acumulativo de los intereses se ha de compensar con una aplicación de un tipo más pequeño que el proporcional en función de la frecuencia de cómputo de intereses. Todo esto se puede apreciar en el siguiente ejemplo, consistente en determinar el montante resultante de invertir 1.000 euros durante 1 año en las siguientes condiciones:
- Interés anual del 12%
Cn = 1.000 x (1 + 0,12)1 = 1.120,00 - Interés semestral del 6%
Cn = 1.000 x (1 + 0,06)2 = 1.123,60 - Interés trimestral del 3%
Cn = 1.000 x (1 + 0,03)4 = 1.125,51
Los resultados no son los mismos, debido a que la capitalización de los intereses se está realizando con diferentes frecuencias manteniendo la proporcionalidad en los diferentes tipos aplicados.
Para conseguir que, cualquiera que sea la frecuencia de capitalización, el montante final siga siendo el mismo es necesario cambiar la ley de equivalencia de los tantos.
2.1. RELACIÓN DE TANTOS EQUIVALENTES EN COMPUESTA
Los tantos en compuesta para que resulten equivalentes han de guardar la siguiente relación:
1 + i = (1 + ik) k
donde k es la frecuencia de capitalización, que indica:
- El número de partes iguales en las que se divide el período de referencia que se tome (habitualmente el año).
- Cada cuánto tiempo se hacen productivos los intereses, esto es, cada cuánto tiempo se acumulan los intereses, dentro del período, al capital para producir nuevos intereses.
Esta relación se obtiene a partir de la definición de equivalencia vista anteriormente, obligando a que un capital (C0) colocado un determinado período de tiempo (n años) genere el mismo montante (Cn) con independencia de la frecuencia de acumulación de intereses (i o ik):
Utilizando el tanto anual i, el montante obtenido será:
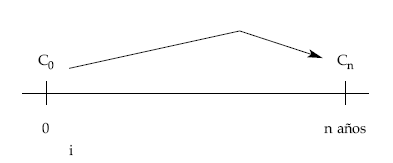
Cn = C0 x (1 + i)n
Utilizando el tanto k-esimal, ik, el montante obtenido será:
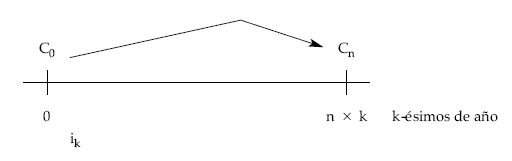
Cn = C0 x (1 + ik)nk
Si queremos que el montante sea el mismo en los dos casos, se tiene que producir la igualdad entre los resultados de ambas operaciones, esto es, dado que la operación es la misma –ya que lo único que ha cambiado es la frecuencia de cálculo de los intereses–, se debe conseguir el mismo capital final en ambos casos, por tanto, obligando a que se cumpla esa igualdad de montantes:
C0 x (1 + i)n = C0 x (1 + ik)nk
Simplificando la igualdad, eliminando C0 y la potencia n:
C0 x (1 + i)n = C0 x (1 + ik)nk
Quedando finalmente:
| (1 + i ) = (1 + ik)k |
Expresión que indica la relación en la que han de estar los tantos, i e ik, para que produzcan el mismo efecto, es decir, para que sean equivalentes.
El valor de i en función de ik será:
| i = (1 + ik)k – 1 |
El valor de ik en función de i será:
| ik = (1 + i)1/k – 1 |
EJEMPLO 6
Determinar el montante resultante de invertir 1.000 euros durante 1 año a un tanto del 12% efectivo anual, suponiendo:
- Devengo anual de intereses:
i = 0,12
Cn = 1.000 x (1 + 0,12)1 = 1.120,00 € - Devengo semestral de intereses:
Puesto que el tipo que se conoce es anual y ahora la frecuencia de cálculo es semestral, habrá que calcular previamente el tanto semestral equivalente al anual de partida, para después calcular el montante.
i2 = (1 + 0,12)1/2 – 1 = 0,05830
Cn = 1.000 x (1 + 0,05830)2 = 1.120,00 € - Devengo trimestral de intereses:
Igual que en el caso anterior, habrá que calcular el tanto trimestral equivalente al anual conocido.
i4 = (1 + 0,12)1/4 – 1 = 0,028737
Cn = 1.000 x (1 + 0,028737)4 = 1.120,00 €
Los resultados son los mismos, debido a la utilización de intereses equivalentes.
3. TANTO NOMINAL (JK)
Por una parte, nos encontramos con la necesidad de aplicar la relación anterior de equivalencia de tantos si queremos que, aun trabajando en diferentes unidades de tiempo, los resultados finales sigan siendo idénticos. Por otra, hay que ser conscientes de la dificultad que supone el conocer y aplicar dicha expresión de equivalencia. En este punto surge la necesidad de emplear un tanto que permita pasar fácilmente de su unidad habitual (en años) a cualquier otra diferente y que financieramente resulte correcta: el tanto nominal.
El tanto nominal se define como un tanto teórico que se obtiene multiplicando la frecuencia de capitalización k por el tanto k-esimal:
Jk = ik x k
Expresión pensada para pasar fácilmente de un tanto referido al año (el tanto nominal) a un tanto efectivo k-esimal, ya que el tanto nominal es proporcional.
Así pues, en compuesta, los tantos de interés pueden ser tantos efectivos (i o ik) o nominales (Jk), teniendo en cuenta que el tanto nominal (también conocido como anualizado) no es un tanto que realmente se emplee para operar: a partir de él se obtienen tantos efectivos con los que sí se harán los cálculos necesarios.
A continuación se muestran las relaciones existentes entre tantos nominales y tantos efectivos anuales.
Tabla de conversión de tantos nominales a tantos anuales efectivos (TAE)
La fórmula de cálculo es:
i = (1 + ik)k – 1 = (1 + Jk/k)k – 1
Frecuencia de capitalización
|
| k = 1 | k = 2 | k = 4 | k = 12 |
| Interés nominal | Anual | Semestral | Trimestral | Mensual |
| 8% | 8,000% | 8,160% | 8,243% | 8,300% |
| 9% | 9,000% | 9,202% | 9,308% | 9,381% |
| 10% | 10,000% | 10,250% | 10,381% | 10,471% |
| 11% | 11,000% | 11,303% | 11,462% | 11,572% |
| 12% | 12,000% | 12,360% | 12,551% | 12,683% |
El tipo de interés efectivo anual correspondiente a un tipo nominal aumenta a medida que aumenta el número de capitalizaciones anuales. Es decir, cada tipo nominal está calculado para trabajar en una determinada unidad de tiempo y sólo en ésa; si se quiere cambiar a otra unidad distinta, habrá que volver a recalcular el tanto nominal, para que el resultado final no cambie.
Tabla de conversión de tantos efectivos anuales (TAE) a tantos nominales
La fórmula de cálculo es: Jk = ik x k = [(1 + i)1/k – 1] x k
Frecuencia de capitalización
|
| k = 1 | k = 2 | k = 4 | k = 12 |
| Interés | Anual | Semestral | Trimestral | Mensual |
| 8% | 8,000% | 7,846% | 7,771% | 7,721% |
| 9% | 9,000% | 8,806% | 8,711% | 8,649% |
| 10% | 10,000% | 9,762% | 9,645% | 9,569% |
| 11% | 11,000% | 10,713% | 10,573% | 10,482% |
| 12% | 12,000% | 11,660% | 11,495% | 11,387% |
El tipo de interés nominal correspondiente a un tipo efectivo anual disminuye a medida que aumenta el número de capitalizaciones anuales.
Igual que antes, si queremos conseguir un mismo tanto efectivo anual a partir de un tanto nominal, éste deberá ser diferente en función de la frecuencia de capitalización para la cual se haya calculado.