La definición de límite es muy parecida a la de límite cero:
Formalizando
Definición: límite de una sucesión (1)
Una sucesión $a_n$ tiene límite $L$ si para cada entorno centrado en $L$ (por pequeño que sea), es posible encontrar un término de la sucesión $a_p$ de modo que todos los términos a partir de $a_p$ pertenecen a dicho intervalo. Si una sucesión $a_n$ tiene límite $L$, lo escribiremos de cualquiera de las tres formas siguientes:
$a_n\rightarrow L \quad\quad \lim a_n = L\quad\quad \lim_{n\rightarrow \infty} a_n =L$
Definición: convergencia - divergencia
Una sucesión que tiene por límite un número (cero o distinto de cero) se llama sucesión convergente. Una sucesión que tiene por límite $+\infty$ o $-\infty$ es una sucesión divergente.
Observa la siguiente animación:
Como ves, $a_n$ está en el intervalo centrado en $L$ y de radio $r$ es equivalente a:
$a_n\in(L-r,L+r)\Longleftrightarrow |a_n-L|\in(-r,r) \Longleftrightarrow |a_n-L|<r$.
De donde deducimos las siguientes dos definiciones equivalentes de límite:
Definición: límite de una sucesión (2)
Una sucesión $a_n$ tiene límite $L$ si para cada $r>0$ (radio de un intervalo), existe un $p$ de modo que $|a_n-L|<r$ si $n\geq p$.
Definición: límite de una sucesión (3)
Una sucesión $a_n$ tiene límite $L$ si la sucesión $a_n-L$ tiene límite 0.
Veamos algunos ejemplos sencillos:
$a_n=1+\frac{1}{n}$
$\lim 1+\frac{1}{n}=1$ porque la sucesión $a_n-1=1+\frac{1}{n}-1=\frac{1}{n}$ tiene límite cero
$b_n=\frac{n+2}{2n+3}$
$\lim \frac{n+2}{2n+3}=\frac{1}{2}$ porque $b_n-\frac{1}{2}=\frac{n+2}{2n+3}-\frac{1}{2}=\frac{1}{4n+6}$ tiene límite cero.
$c_n=\frac{4n-2}{n}$
La sucesión $c_n=\frac{4n-2}{n}$ tiene límite $4$ pues $c_n=\frac{4n-2}{n}=4-\frac{2}{n}$ y por tanto $c_n-4=\frac{-2}{n}$, que tiene por límite cero.
Ahora te toca a ti. Resuelve las siguientes actividades sobre límites, sucesiones convergentes y divergentes:
Actividades de consolidación
Resuelve las siguientes actividades sobre límites de sucesiones, sucesiones convergentes y divergentes:
- Justifica el valor de los siguientes límites:
- $\lim \frac{n+1}{n}=1$
- $\lim \frac{n^2+3}{3n^2}=\frac{1}{3}$
- $\lim \frac{1-n}{1+n}-3=-4$
- $\lim \frac{1}{n^2+n}=0$
- $\lim \frac{n^2+2n}{n}=\infty$
- Escribe tres sucesiones que tengan por límite, respectivamente, 0, 11 y -4.
- ¿Es cierto que una sucesión o bien es convergente o bien es divergente? (Indicación: observa el comportamiento de la sucesión $a_n=(-1)^n$.
- De una sucesión sabemos que es convergente y que tiene infinitos términos positivos y también infinitos términos negativos. ¿Cuál es su límite?
- Calcula el límite de las siguientes sucesiones. Para ello, en primer lugar conjetura el posible valor del límite utilizando las estrategias que conoces (comparándola con otra sucesión, representándola gráficamente, utilizando una idea intuitiva del comportamiento del término general de la sucesión...) Después debes justificar el valor del límite conjeturado.
- $\lim \frac{2n+1}{3n}$
- $\lim \frac{(3n-1)^2}{7n^2+3}$
- $\lim \frac{2n(n-1)}{n^2-1}$
Una cuestión teórica
Demuestra que si una sucesión $a_n$ tiene límite, éste debe ser único.
Imagina que la sucesión $a_n$ tuviera dos límites $L_1$ y $L_2$. Supón, por ejemplo, que $L_1<L_2$. Siempre es posible encontrar dos entornos centrados, uno en $L_1$ y otro en $L_2$ que no se corten:
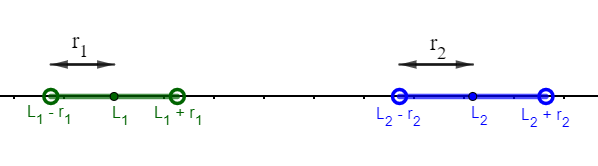
¿Dónde estarían los términos de la sucesión $a_n$ si su límite fuese simultáneamente $L_1$ y $L_2$?
Licencia: licencia propietaria