–¿Cuántas horas al día duraban esas lecciones?–preguntó Alicia interesada [...]
–Teníamos diez horas al día el primer día. Luego, el segundo día, nueve, y así sucesivamente.
–Pues me resulta un horario muy extraño –observó la niña–. Entonces el día once sería fiesta, claro.
–Naturalmente que sí –respondió la Falsa Tortuga.
-¿Y el duodécimo?
Lewis Carrol
Idea intuitiva de límite
Muchas veces no podemos determinar de manera exacta el valor de una determinada cantidad y lo que hacemos es buscar una aproximación. Si no hacemos una sola aproximación sino una serie de ellas, cada una un poquitín más precisa que la anterior, es de esperar que nos estemos aproximando cada vez más al valor buscado.
Los siguientes ejemplos ilustran esta situación de una forma más precisa:
 |  |  |  |
Aproximando el área bajo una recta
- Duración:
- 30 minutos
- Agrupamiento:
- grupos de 4 o 5 alumnos
Observa la siguiente figura.
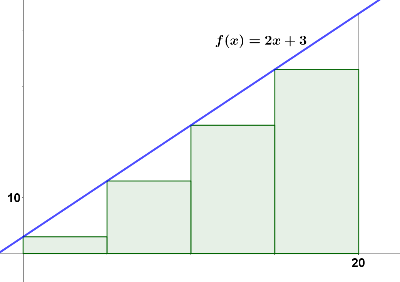
Los rectángulos se han obtenido dividiendo el intervalo [0,20] en 4 partes guales. Los 4 rectángulos tienen la misma base y su altura está sobre la gráfica de la función y=2x+3.
- Comprueba que la suma de sus áreas es 360.
Denotemos a esta suma como $S_4$. La suma de las áreas de los cinco rectángulos siguientes será, por tanto $S_5$:
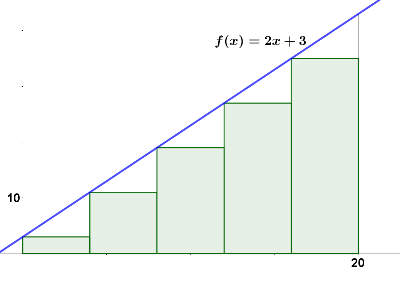
- Determina $S_5$, esto es, la suma de las áreas de los cinco rectángulos de la figura anterior.
- Calcula el valor de los términos $S_2$, $S_{10}$, $S_{20}$ y $S_{40}$.
- ¿A qué valor crees que se aproximará $S_n$ cuando el número de rectángulos $n$ crezca?
Para cada valor de $n$ (fijado el número de rectángulos), el área de los rectángulos sigue una progresión aritmética.
- Recuerda en qué consiste una progresión aritmética
Para calcular, por tanto $S_n$, deberás sumar los $n$ términos consecutivos de una progresión aritmética.
- Busca la expresión que sirve para calcular la suma de los $n$ primeros términos de una progresión aritmética.
En el siguiente applet puedes comprobar las soluciones de las distintas sumas pedidas en la actividad:
Cuadratura de una parábola
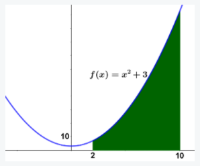
Se considera una sucesión definida como el problema anterior, pero para rectángulos construidos bajo la gráfica de la función $g(x)=x^2+3$ entre los valores de abscisas $x=2$ y $x=10$.
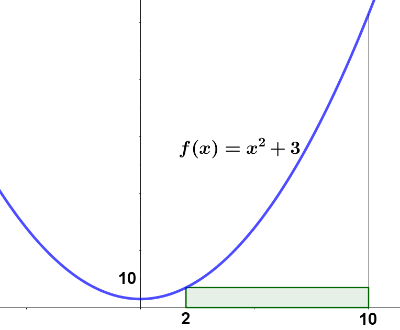 | 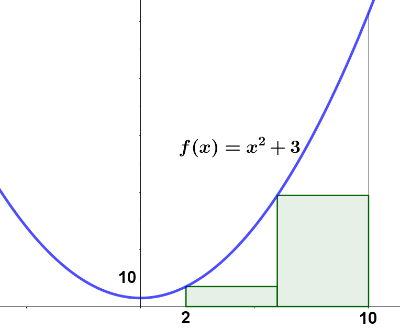 | 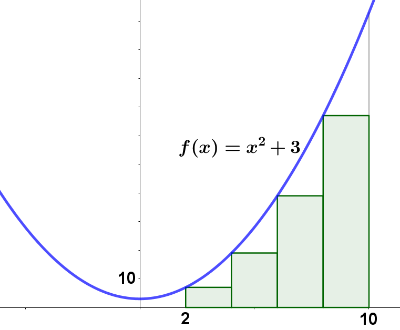 | 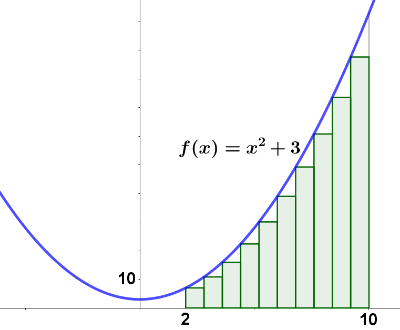 |
- Calcula el valor de los términos $S_1$, $S_2$, $S_4$, y $S_{10}$.
- A mediada que $n$ toma valores cada vez más grandes, $S_n$ ¿crecerá sin límite? ¿Por qué?
- ¿Puedes encontrar un ejemplo de un valor que no pueda superar nunca ningún término de la sucesión $S_n$?
- Si la sucesión $S_n$ tiene límite, ¿qué representa este límite?
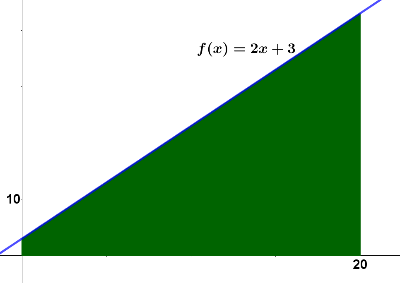
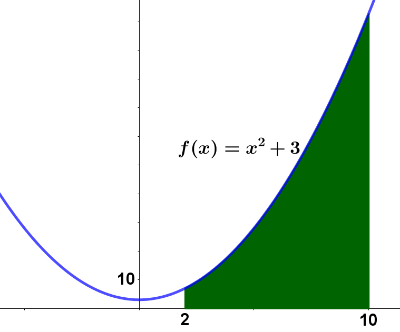
La respuesta a la cuarta pregunta tiene una gran importancia. Hay veces que necesitamos determinar el área debajo de una curva y lo podemos hacer mediante las técnicas habituales (figura de la izquierda). Hay otras muchas, como en el caso de nuestra parábola $y=x^2+3$ en las que esto es imposible (figura de la derecha).
 |  |
Este problema, encontrar el área bajo una parábola, se le conoce como el problema de la cuadratura de la parábola, y fue resuelto por primera vez por Arquímedes, hace más de 2200 años.
Si quieres comprobar que has calculado bien las sumas de los rectángulos, puedes hacerlo con el siguiente applet hecho con GeoGebra:
Calculando cifras decimales de Pi
Como sabes, el número $\pi$ puede definirse como el cociente entre el perímetro de una circunferencia y su diámetro. El objetivo de esta tarea es encontrar una aproximación del valor de $\pi$. Vamos a inscribir para ello una sucesión de polígonos en la circunferencia.
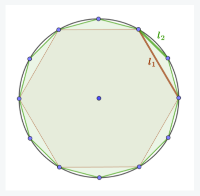
Considera una circunferencia de radio unidad, $r=1$. Imagina que tienes construido un hexágono regular inscrito a ella, como en la figura:
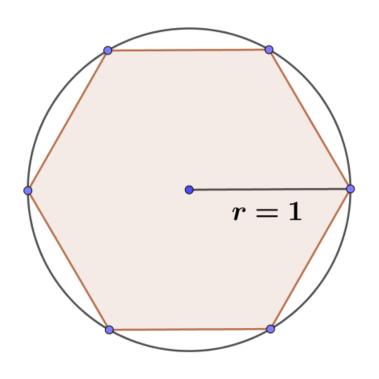
- ¿Cuánto vale el perímetro del hexágono?
Llamemos $a_1$ a este perímetro. Si te fijas, el perímetro del hexágono es un poquitín menor que el de la circunferencia, por lo que tenemos la primera aproximación de $\pi$ (algo tosca, eso sí):
$$\pi\simeq \frac{a_1}{2}$$
A partir del hexágono, podemos construir un nuevo polígono inscrito al de la circunferencia, con el doble de lados. No hay más que situar un punto entre cada dos del hexágono sobre la circunferencia:
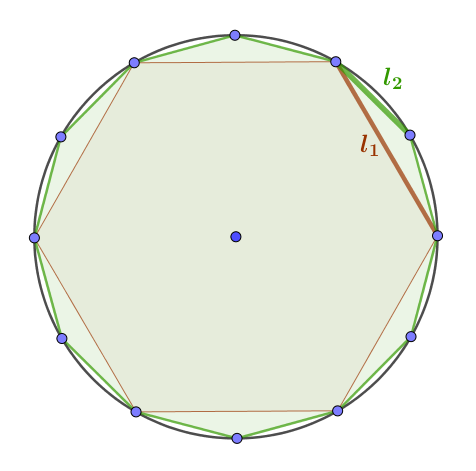 | 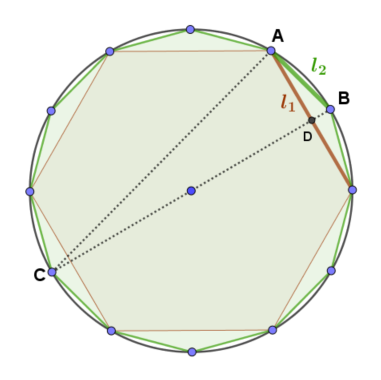 |
Observando la figura de la derecha, responde a las siguientes cuestiones:
- ¿Eres capaz de encontrar tres triángulos rectángulos en la figura? ¿Por qué son rectángulos?
- Calcula la longitud del segmento DB en función de las longitudes $l_1$ y $l_2$.
- Los triángulos ADB y ACB son semejantes. ¿Eres capaz de justificar por qué?
- A partir del hecho de que ADB y CAB son semejantes, determina la medida de $l_2$ en función de $l_1$.
Una vez calculado el nuevo lado $l_2$, puedes calcular de forma inmediata el perímetro del dodecágono, al que denotamos $a_2$. El dodecágono se acerca más a la circunferencia que el hexágono, así que tenemos una nueva y mejor aproximación de $\pi$:
$$\pi\simeq \frac{a_2}{2}$$
Si repetimos la anterior construcción una vez más, podemos calcular el perímetro del polígono de 24 lados, $a_3$, el perímetro del polígono de 48 lados, $a_4$ y así sucesivamente. Hemos obtenido una sucesión de perímetros de polígonos inscritos a nuestra circunferencia $\{a_1,a_2,a_3,\ldots\}$.
- ¿A qué valor se acercarán los términos de la sucesión $\{a_n\}$ a medida que tomemos valores de $n$ grandes?¿por qué?
- Determina las aproximaciones de $\pi$ que se consiguen con estos valores $a_3$ y $a_4$. ¿Qué tal se acercan al valor de $\pi$ que conoces?
La sucesión de Fibonnacci
- Duración:
- 10 minutos
- Agrupamiento:
- grupos de 4 o 5 alumnos
A la sucesión
$1,1,2,3,5,8,13,\ldots$
se le conoce como sucesión de Fibonnacci.
- ¿Cómo se construyen los términos de esta sucesión?
- ¿Eres capaz de añadir tres nuevos términos?
- ¿Qué le ocurre a los términos de esta sucesión $a_n$ cuando tomamos valores de $n$ muy grandes? ¿Se acercan a algún valor?
- ¿Crees que existirá algún término de la sucesión que sea mayor que $1 872 342$?
- ¿Crees que existirá algún término de la sucesión que sea mayor que $1 872 342^{1 872 342}$?
Licencia: licencia propietaria