En la siguiente imagen puedes ver la sucesión $a_n=\frac{1}{n}$. Como sabes, $\lim_{n\rightarrow \infty}a_n=0$, pues los términos $\frac{1}{n}$ podemos "hacerlos tan cercanos a cero como queramos".
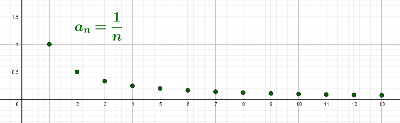
Consideremos una segunda sucesión de términos positivos: $b_n=\frac{1}{n+2}$. Como sabes, $0<\frac{1}{n+2}<\frac{1}{n}$ para cualquier natural $n\in \mathbb{N}$.
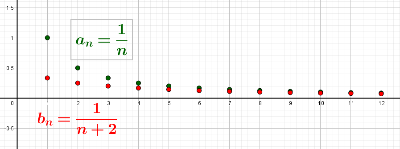
- ¿Qué podemos decir del valor del límite $\lim_{n\rightarrow \infty}\frac{1}{n+2}$?
 Vamos a aplicar la regla del sandwich en algunos casos prácticos.
Vamos a aplicar la regla del sandwich en algunos casos prácticos.